Benford's Law as a Fraud Detection technique
Recently, I picked up a handy technique for narrowing down the dataset to look for fraud anomalies - Benford’s Law. It basically states that, in a collection of naturally occurring numerical values, the frequency of the first digit follows a exponential decreasing trend as digit goes from 1 to 9.
What? In simple terms, in a list of numbers, if we determine the counts of all the first digits - 1 to 9, then we should see rapidly decreasing counts from 1 to 9.
How, do you ask, do we know, it follows such a pattern? Well because of, some careful observation by a curiosity driven scientist, followed by experimentation and defining it into mathematical form - in short, SCIENCE.
Maybe some examples will make it explicable. Here you go.
- Food prices
I got to know about this data from a mailing list I follow - Data is Plural by Jeremy Singer-Vine.
The UN World Food Programme’s vulnerability analysis group collects and publishes food price data for more than 1,000 towns and cities in more than 70 countries. The dataset, which goes back more than a decade, covers basic staples, such as wheat, rice, milk, oil, and more. It’s updated monthly and feeds into (among other things) the UNWFP’s price-spike indicators.
Here’s the Benford plot I got from the data. There were 743,914 records in total. To see a lot of other exploration around the data along with the Benford’s, you can look at this jupyter notebook - Benford’s Analysis: Global Food Prices.
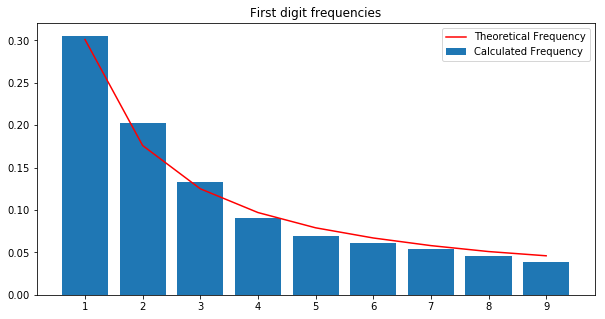
- State Elections India
Again through Data is Plural mailing list. Five states in India, representing nearly 250 million residents — Punjab, Uttar Pradesh, Uttarakhand, Goa, and Manipur - have already held legislative assembly elections this year. India’s Election Commission publishes these results, but only as webpages. A couple of Hyderabad-based developers have scraped the website, and published CSVs of the data on GitHub.
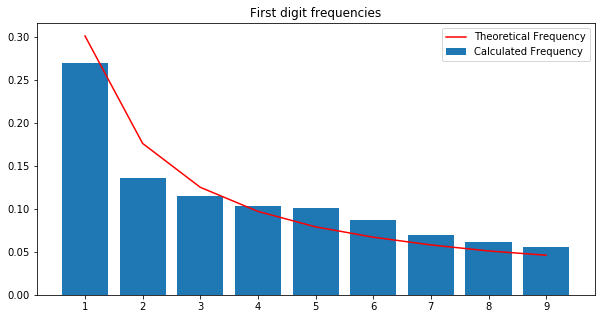
Above is the Benford plot for the number of votes per constituency. There were 7,849 records, pertaining to various constituencies for 5 states against each political party. As you can see it follows the Benford’s trend. For more exploration on the data you can have a look at this notebook - Benford’s Analysis: State Elections India
Okay, so it does work. Is it that simple? Sure it is, but there are some conditions. These conditions are not something which are always correct, but most of the times, they are.
-
The more orders of magnitude the data evenly covers the more accurate the law will be. (uniform distribution; orders of magnitude)
Some real world distributions those follow this rule are - population of villages, stock prices, food prices (we discussed this example above). Some others that won’t follow the rule would be - heights of human adults, IQ scores, temperature measurements (we will discuss this example later in the post).
-
When the data has right skew. (mean > median; long right tail)
Basically, when there is a long right tail in the distribution. This happened in the above 2 examples. (Checkout the notebook links. Why do you think they were there?)
-
Number resulting from mathematical combinations.
Eg. price x quantity
-
Transactional level data.
Eg. Sales, reimbursements, spendings
-
Data has no pre-defined minimum and maximum
-
Normal distributions don’t follow the Benford’s law.
We’ll see this demonstration below.
-
Sequential quantities wont follow the Benford’s law
Any example of where it doesn’t work? Here you go.
Temperatures
I cant find the link for the dataset used. It was an open dataset I had downloaded some 7-8 months back. I had downloaded just for the India category. It consists of the temperatures from 1700’s to present (with a lot of NaNs for earlier periods). Here’s the notebook - Benford’s Analysis: Climate - which has a lot of details around the Benford’s analysis. Here are the final plots.
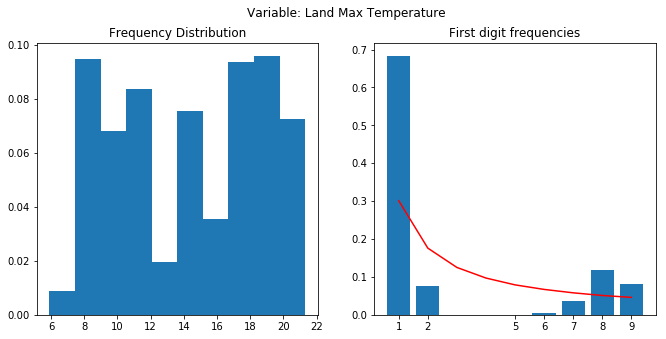
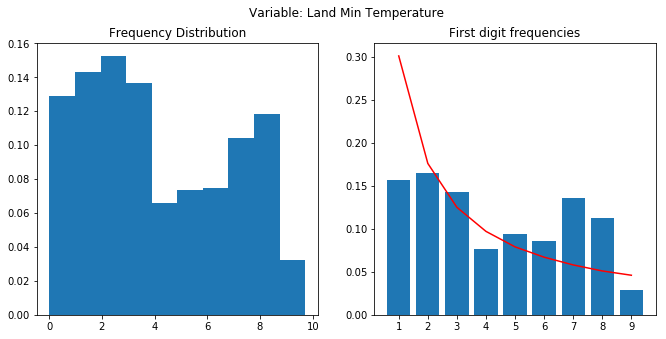
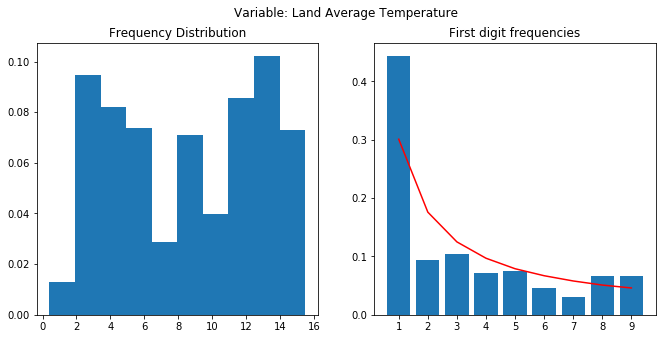
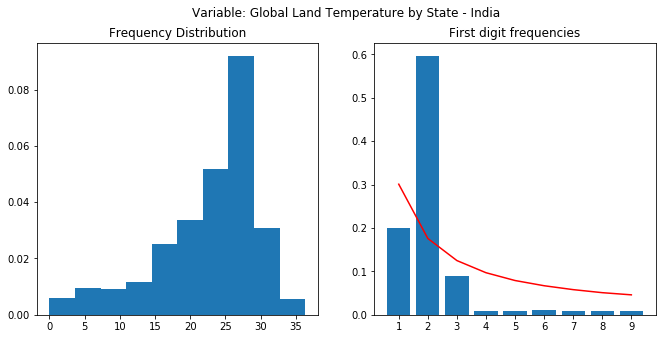
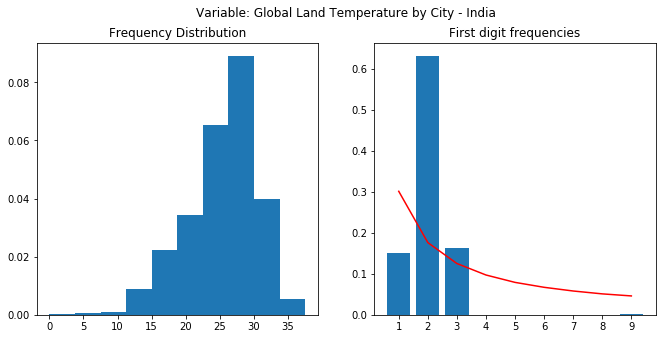
As you can see, none of the plots show a proper following of the Benford’s law. The frequencies should have a decreasing trend as we move from 1 to 9. Data has a predefined low and high. Last to plot were almost normally distributed. A lot of “nays” where there. Notebook dives deeper into the analysis.
Now, we have come to a million dollar question. Like literally, it can help us save millions of dollars (or to discover that they are lost?).
How does the Benford’s Analysis help with fraud?
Assuming the data should follow the Benford’s law, there can be 2 reasons when it wont follow it - legitimate and fraudulent. Obviously.
Legitimate reasons can be - merging of low-figure amounts or something (service, product) that has to be paid frequently and has a fixed rate/price. These cases will throw off the Benford’s trend.
Fraudulent reason is something we are interested in. It is based on the fact that, a fraudster, to maximize his/her gains, would put in a larger value (starting with 8 or 9). Or, if a person is using values starting with ones then usually, they keep rounded values. So, Benford’s law can also be done for 2nd digit. It’s been generalized for any number of digits, but second digit is mostly enough. And, if it has been done a lot of times then the frequencies wont be in line with Benford’s. So, using Benford’s law doesn’t exactly give us anomalies, it just narrow down the dataset to something more manageable.
Conclusion
Benford’s law is a great technique to get a subset where you are likely to find some fraudulent transactions. It’s not guaranteed to work every time, but it’s really inexpensive to perform. If the trend seems to be way off from the ideal one then there you have something to look else just move on.
PS. Benford’s Law is a special case of Zipf’s Law. There is a very cool video from vsauce - The Zipf Mystery